TP4 - Aprendizado supervisionado

Introdução

Nesse projeto você irá implementar uma rede neural artificial (RNA) de 3 camadas (1 de entrada, 1 escondidada e 1 de saída) para classificação de dígitos escritos manualmente. Para isso, você irá treinar a sua RNA no conjunto de dados [MNIST], que possui 70.000 imagens com resolução 28x28 dos dígitos de 0 a 9. O objetivo é praticar a modelagem e a implementação de RNAs, bem como analisar os resultados desse tipo de algoritmo, em particular o impacto dos parâmetros do algoritmo no desempenho do agente.

Código-base

Executar servidor

Clique aqui para baixar o código-base, que inclui um cliente em JavaScript para configurar os hiperparâmetros da RNA e iniciar seu treinamento, além de salvar e carregar resultados (pesos e curva de aprendizado). O código também contém um servidor em Python para implementar e executar o treinamento da RNA. Para executar o servidor, você precisará instalar as dependências do projeto e iniciar o servidor com os seguintes comandos:

pip install -r requirements.txt # Instalar dependencias
python3 server.py -port 5001 # Executar o servidor

Assim que o servidor iniciar, você pode abrir o seguinte endereço em qualquer navegador: http://localhost:5001.

Tarefas

Todas as suas tarefas de implementação serão realizadas no arquivo learn.py. Antes de começar sua implementação, abra esse arquivo e se familiarize com as funções definidas nesse arquivo. Em seguida, estude a função gradient_descent_step() do arquivo serve.py, pois ela que executa as funções que terá que implementar.

1. Inicialização dos parâmetros (pesos)

Implemente a função initialize_parameters(input_size, hidden_size, output_size) para inicializar os parâmetros (pesos) da RNA. Os parâmetros input_size, hidden_size, output_size representam o número de neurônios nas camadas de entrada, encondida e de saída, respectivamente. Como o MNIST tem dígitos de 0 a 9, temos um problema de classificação multiclasse com C=10 classes. Sendo assim, o número de neurônios da camada de saída será output_size = 10. Além disso, como as imagens de entrada tem 28x28 pixels de resolução, o número de neurônios na camada de entrada será input_size = 28x28 = 784. A número de neurônios da camada escondida é um hiperparâmetro configurado no cliente no campo de entrada Neurônios (camada escondida).

Essa função deve retornar uma tupla com quatro arranjos numpy: (W1, b1, W2, b2), onde W1, b1 são os pesos da primeira camada e W2, b2 os pesos da segunda. Lembre-se que em RNAs precisamos inicializar os pesos W com valores aleatórios próximos de zero. Os pesos b podem ser inicializados com zero, sem problemas. Portanto, utilize a função np.random.randn do numpy para inicializar os pesos W e a função np.zeros para os pesos b. O tamanho das matrizes W1 e W2 devem ser input_size x hidden_size e hidden_size x output_size, respectivamente. O tamanho dos vetores b1 e b2 devem ser 1 x hidden_size e 1 x output_size, respectivamente. Como os pesos W devem ser inicializados próximos de zero, multiplique o resultado da função np.random.randn por 0.01.

Resultados esperados

W1, b1, W2, b2 = learn.initialize_parameters(784, 4, 10)
----
W1: (784, 4)
[[ 0.00496714 -0.00138264  0.00647689  0.0152303 ]
 [-0.00234153 -0.00234137  0.01579213  0.00767435]
 [-0.00469474  0.0054256  -0.00463418 -0.0046573 ]
 ...
 [-0.00139397  0.00739653 -0.01909356  0.01318302]
 [ 0.00072681 -0.00411493 -0.00089234 -0.00037571]
 [-0.01731201  0.01494938  0.00041326  0.00443002]]

b1: (1, 4)
[[0. 0. 0. 0.]]

W2: (4, 10)
[[ 0.0095155  -0.01021162  0.00473472 -0.00267641  0.00846771 -0.02127227
  -0.00099094 -0.00602821  0.00432263  0.00470044]
 [-0.00707626 -0.00712174 -0.00110665 -0.00896642  0.00841984 -0.00369207
  -0.02906988 -0.00374822 -0.01038544 -0.01631276]
 [-0.01237427  0.00109408  0.01328641  0.00313184 -0.00606503  0.00455904
  -0.0045909  -0.006946   -0.01154363 -0.01751829]
 [-0.00389924  0.00158053 -0.00096624 -0.00415967 -0.00945746  0.00608246
  -0.01317132  0.00776028 -0.01002217 -0.00752435]]

b2: (1, 10)
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]

2 Funções de ativação

Antes de implementar a propagação das entradas, você precisa implementar as funções de ativação da sua RNA. Nesse trabalho, usaremos a relu como ativação da camada escondida e a softmax para a camada de saída, pois temos um problema multiclasse.

2.1 Relu

Implemente a função relu(z) com a ativação relu, como visto em sala de aula:

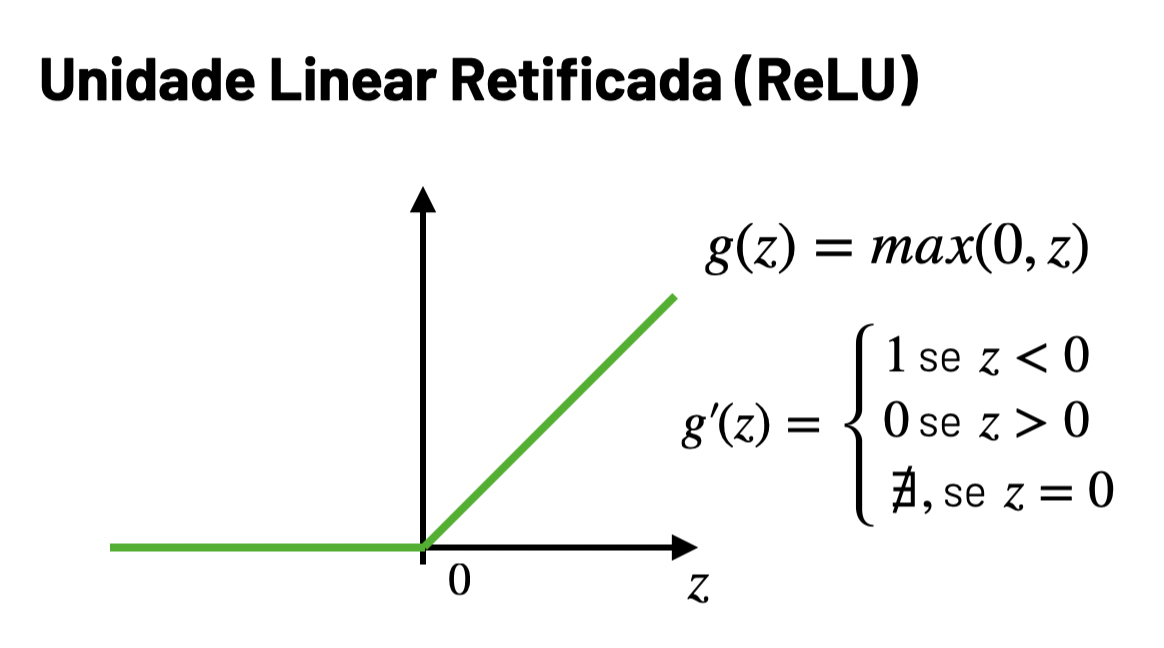
2.2 Softmax

Implemente a função softmax(z) com a ativação softmax para , como visto em sala de aula:

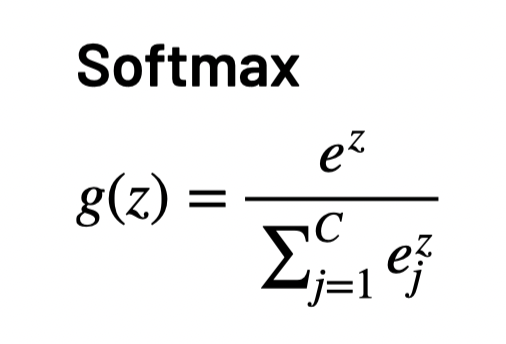
Resultados esperados

a = learn.relu(np.array([[-1, 0, 1], [-2, 0, 2]]))
----
a: [[0 0 1]
    [0 0 2]]

a = learn.softmax(np.array([[1, 2, 3], [4, 5, 6]]))
----
a: [[0.09003057 0.24472847 0.66524096]
    [0.09003057 0.24472847 0.66524096]]

3. Propagação das entradas

Implemente a função forward(X, parameters) para propagar as entradas X pela RNA definida pelos parâmetros parameters (tupla com (W1, b1, W2, b2)). Para facilitar o cálculo dos gradientes, é importante calcular a ativação de cada camada em duas etapas: (i) combinação linear e (ii) função de ativação. Portanto, calcule primeiro a combinação linear da camada escondida Z1 = XW1 + b1 e em seguida aplique a função relu para calcular sua ativação A1 = relu(Z1). Faça a mesma coisa para a camada de saída, calculando primeiro Z2 e depois A2. Note que a entrada da camada de saída é a ativação da camada escondidade A1, e não a matrix de exemplos X. A funcão forward deve retornar uma tupla (Z1, A1, Z2, A2). Utilize a função np.dot para fazer as multiplicações de matrizes XW1 e A1W2.

Resultados esperados

X = np.random.randn(2, 784)
Z1, A1, Z2, A2 = learn.forward(X, parameters)
----
Z1: (2, 4)
[[ 0.24242511 -0.1806328  -0.32022768  0.05051037]
 [-0.3853982  -0.13327416  0.02946697  0.13882065]]

A1: (2, 4)
[[0.24242511 0.         0.         0.05051037]
 [0.         0.         0.02946697 0.13882065]]

Z2: (2, 10)
[[ 0.00210984 -0.00239572  0.00109901 -0.00085894  0.00157509 -0.00484971
  -0.00090552 -0.00106941  0.00054169  0.00075945]
 [-0.00090593  0.00025165  0.00025738 -0.00048516 -0.00149161  0.00097871
  -0.00196373  0.00087261 -0.00173144 -0.00156075]]

A2: (2, 10)
[[0.10025104 0.09980037 0.10014976 0.09995386 0.10019745 0.09955576
  0.09994921 0.09993283 0.10009396 0.10011576]
 [0.09996714 0.10008293 0.1000835  0.10000921 0.09990861 0.10015572
  0.09986145 0.10014509 0.09988465 0.0999017 ]]

4. Função de perda

Implemente a função cross_entropy_loss(y_true, y_pred) para calcular a entropia cruzada entre a distribuição real de rótumos y_true e as previsões da RNA y_pred. Como visto em sala de aula, a função de perda é definida da seguinte maneira:

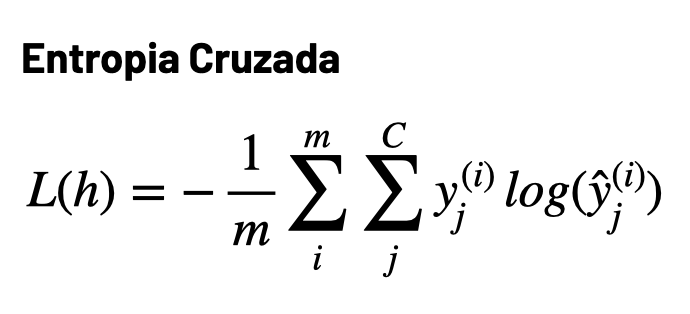
Utilize a função np.log para calcular o logarítmo e np.sum para o somatório.

Resultados esperados

y_true = np.array([[0, 1, 0], [1, 0, 0]])
y_pred = np.array([[0.1, 0.6, 0.3], [0.3, 0.4, 0.3]])
loss = learn.cross_entropy_loss(y_true, y_pred)
----
loss: 0.8573992140459634

5. Gradiente descendente

Implemente a função gradient_descent_step(X, y, parameters, learning_rate) para executar uma única época do gradiente descendente:

Utilize a função forward() para propagar as entradas X pela RNA
Calcule o erro l de previsão atual com a função cross_entropy_loss()
Calcule os gradientes com a função backward() (já está implementado para você)
Atulize os pesos W1, b1, W2, b2 com a regra de atualização do gradiente descendente w = w - alpha dw

A sua função deve retornar uma tupla com pesos atualizados (W1, b1, W2, b2) e o erro atual l da rede, nessa ordem.

Resultados esperados

X = np.random.randn(2, 784)
y = np.array([[0, 1, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 1, 0, 0]])
parameters = (W1, b1, W2, b2)
parameters, loss = learn.gradient_descent_step(X, y, parameters, learning_rate=0.01)
----
loss: 2.3007908193979407

W1: (784, 4)
[[ 0.00489277 -0.0013802   0.00647982  0.01522034]
 [-0.00232832 -0.00234474  0.01579393  0.00766823]
 [-0.00470117  0.00545288 -0.00465534 -0.00458549]
 ...
 [-0.00136562  0.00739478 -0.01909403  0.01318462]
 [ 0.00067495 -0.00411447 -0.00088931 -0.00038599]
 [-0.01731262  0.01497452  0.0003934   0.00449739]]

b1: (1, 4)
[[-4.63539605e-05  2.45369176e-05 -1.63779507e-05  5.55761532e-05]]

W2: (4, 10)
[[ 0.00950049 -0.01007663  0.0047197  -0.00269141  0.00845266 -0.02128728
  -0.00100588 -0.00604321  0.00430764  0.00468546]
 [-0.00718544 -0.0062819  -0.00121602 -0.00907558  0.00831039 -0.00380133
  -0.0291786  -0.00371489 -0.01049451 -0.01642172]
 [-0.01248018  0.00098765  0.01317978  0.0030256  -0.00617091  0.00445233
  -0.00469654 -0.00599127 -0.0116493  -0.01762391]
 [-0.00409178  0.00138703 -0.00116009 -0.00435282 -0.00964994  0.00588846
  -0.01336337  0.00949599 -0.01021428 -0.00771637]]

b2: (1, 10)
[[-0.00099922  0.00399859 -0.0010031  -0.00100043 -0.0010005  -0.00100286
  -0.00099571  0.00399782 -0.00099769 -0.0009969 ]]

6. Avaliação do modelo

Como esse é um problema de classificação, você irá avaliar a sua rede usando a acurácia de previsão, isto é, a taxa de acerto da rede no conjunto de teste. Implemente a função accuracy(y_true, y_pred) para calcular a acurácia entre os rótulos reais y_true e as previsões y_pred. Você pode fazer essa implementação de maneira vetorial em uma linha utilizando as funções np.mean e np.argmax do numpy.

Resultados esperados

y_true = np.array([[0, 1, 0], [1, 0, 0]])
y_pred = np.array([[0.1, 0.6, 0.3], [0.3, 0.4, 0.3]])
acc = learn.accuracy(y_true, y_pred)
----
acc: 0.5

7. Relatório

Nesse trabalho prático você não precisa enviar um relatório, no entanto, você precisará enviar dois gráficos, um com a curva de erro e o outro com a curva de acurácia da sua RNA. Para gerar os gráficos, execute o script plot.py, que irá produzir as curvas utilizando os dados dos arquivos model/losses.csv e model/accuracies.csv.

Escolha hiperparâmetros (número de épocas, taxa de aprendizado e número de neurônios na camada escondida) que maximizem a acurácia de teste da RNA. Sua acurácia de teste deve ser de no mínimo 80%. As figuras a seguir mostram exemplos de como os seus gráficos devem ficar:

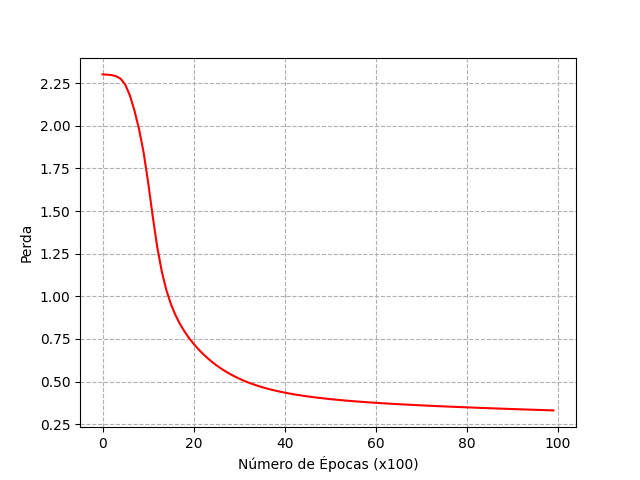
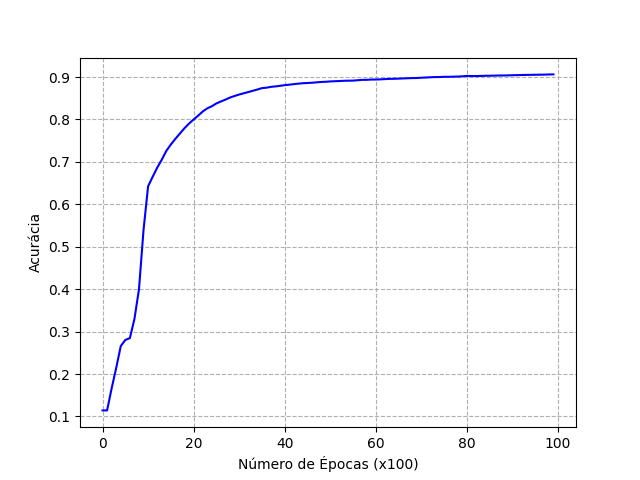
Submissão

Para submeter o seu trabalho, envie o seu arquivo learn.py e as duas imagens losses.png e accuracies.png na tarefa TP4 - Aprendizado supervisionado no PVANet.